Clustering Considered Harmful III: Commensurability

[This is the third in a planned series of posts on clustering that I'll publish over the coming period. The first part is here. When it's finished, I'll collect it all together into a properly printable paper.]

I have always found it surprising that the standard shorthand for a dubious or invalid comparison is apples and oranges. For while, granted, apples and oranges are different in many respects, they're not so different, and a comparison is not completely absurd. I would have thought that fruit flies and symphonies or physicists and personal computers3 or prime numbers and dictionaries might all present more obvious challenges as subjects for meaningful comparison. But perhaps that is the point: people would be unlikely to find themselves inadvertently trying to compare a fruit fly and a symphony4 whereas one can more easily imagine unwittingly comparing, say, a Cox's Orange Pippin with a Seville Orange.

There is a general problem with comparing, and in many cases with combining, so-called non-commensurate variables. The Shorter Oxford English Dictionary defines the adjective commensurate thus:

1. Having the same measure; coextensive. Const. with, to 1641.

2. Of corresponding extent or degree; proportionate, adequate. Const. to, with. 1649.

3. Corresponding in nature (with, to) – 1678.

4. = COMMENSURABLE 1 (rare) 1690.

At the risk of labouring the point, our three spatial dimensions are perfect examples of commensurate quantities: if we lay down an ordinary rectilinear x-y-z coordinate grid, there is a very strong sense in which going one mile parallel to the x-axis is equivalent to travelling one mile parallel to the y-axis or one mile parallel to the z-axis. A mile is a mile is a mile, and we feel very comfortable applying the notion of distance in an arbitrary direction and computing it in the usual Euclidean/Pythagorean manner.

We are on more treacherous ground when our dimensions consist of non-commensurate quantities, as only some of those who study or practise co-called cost-benefit analysis appear to be aware. For the approach of cost-benefit analysis requires us to express all the costs and all the benefits of some proposed course of action (or of some set of alternatives) in terms of a single numéraire—almost always money. Thus, when planning a motorway, we must express not only the financial cost in financial terms, but also such other diverse costs as habitat destruction, contribution to global warming, displacement of families from their homes, increases in pollutive emissions and likely increase in road traffic deaths in pounds, shillings and pence. Similarly, benefits must be expressed in cash terms. To do this, of course, requires suitable equivalences and conversion factors to be put in place (human life lost—£1 million; contestible contribution to possible making of planet uninhabitable by humans at some indeterminate point in the future—£2,452.13). This has led some cynics to suggest that cost-benefit analysis, as practised, is not so much a rational and objective way of collating all relevant evidence and drawing from it the optimal conclusion as a tool for justifying some desired outcome by careful manipulation of the many and infinitely negotiable parameters absolutely required in order for the method to function.

It will not have escaped the reader's attention that we have a similar problem with cluster analysis if we wish to apply it in situations where the factors to be considered as dimensions are not commensurate. Unfortunately, this is almost always the case in marketing, and it this non-commensurability of the inputs, and consequentially necessary setting of many essentially arbitrary conversion factors that forms the first objection to the common application of cluster analysis to customer database segmentation. The clusters that result from a clustering exercise are not merely dependent upon the equivalences and conversion factors chosen for the distance function, but are almost entirely determined by those choices.

As a minimum, this should cause us to treat with extreme scepticism the all-too-common suggestions that cluster analysis impartially and objectively uncovers inherent, underlying or intrinsic structure within the customer data. It might be more accurate to say that it allows the consequences of different choices of equivalence among input variables to be revealed through the mechanism of mapping a distance function to a cluster structure.

David Hand's Example

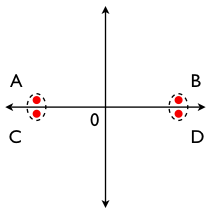
I'll close this post with a graphic illustration of the effect of scaling based on an example provided by David Hand.5 Consider clustering four points, A(–1, 10), B(1, 10), C(–1, –10) and D(1, –10), as sketched below.

Clearly, points A and B form a cluster, as do points C and D. (The within-cluster distances are small and the between-cluster distances are large; these are defining characteristics of a good clustering.)

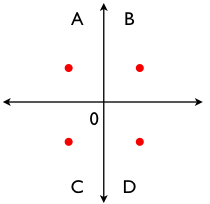
Now let us rescale, multiplying the x-coordinate by 10 and dividing the y-coordinate by the same amount. The result would be the following.

Now, clearly, points A and C form a cluster, while points B and D form another.

Or consider multiplying the original x-coordinate by 5 and dividing the original y-coordinate by 2. Now, our plot looks like this.

Our clusters have disappeared entirely!

To be clear, it is not my claim that clustering is always invalid or meaningless: if the variables were commensurate on the original scale, then A and B really do cluster, as do C and D. The point is that scale is crucial, and extremely problematical when for non-commensurate quantities.

Next up: direction (probably).

Notes

3 Though even as I write this I'm thinking Paul Dirac—definitely a Mac kind of a guy; very concerned with elegance and form; happy to do a few things well; a true hero among a narrow subset of scientists. I hesitate slightly at the prospect of nominating a physicist as the natural Wintel PC analogue, but sticking with fathers of the quantum theory, perhaps Nils Bohr, who arguably thought that the key thing was not to spend too long sweating the details like meaning and elegance but simply to get some computational tools into as many people's hands as possible to allow them to make some progress with the job in hand. ↩

4 'How long is Drosophila melanogaster? Around 2.5mm you say. And Beethoven's Ninth? 74 minutes. Hmm. Let's convert those both to natural units using the speed of light, c as the conversion factor . . .' ↩

5 Discrimination and Classification, D. J. Hand, John Wiley (Chichester), 1981. ↩